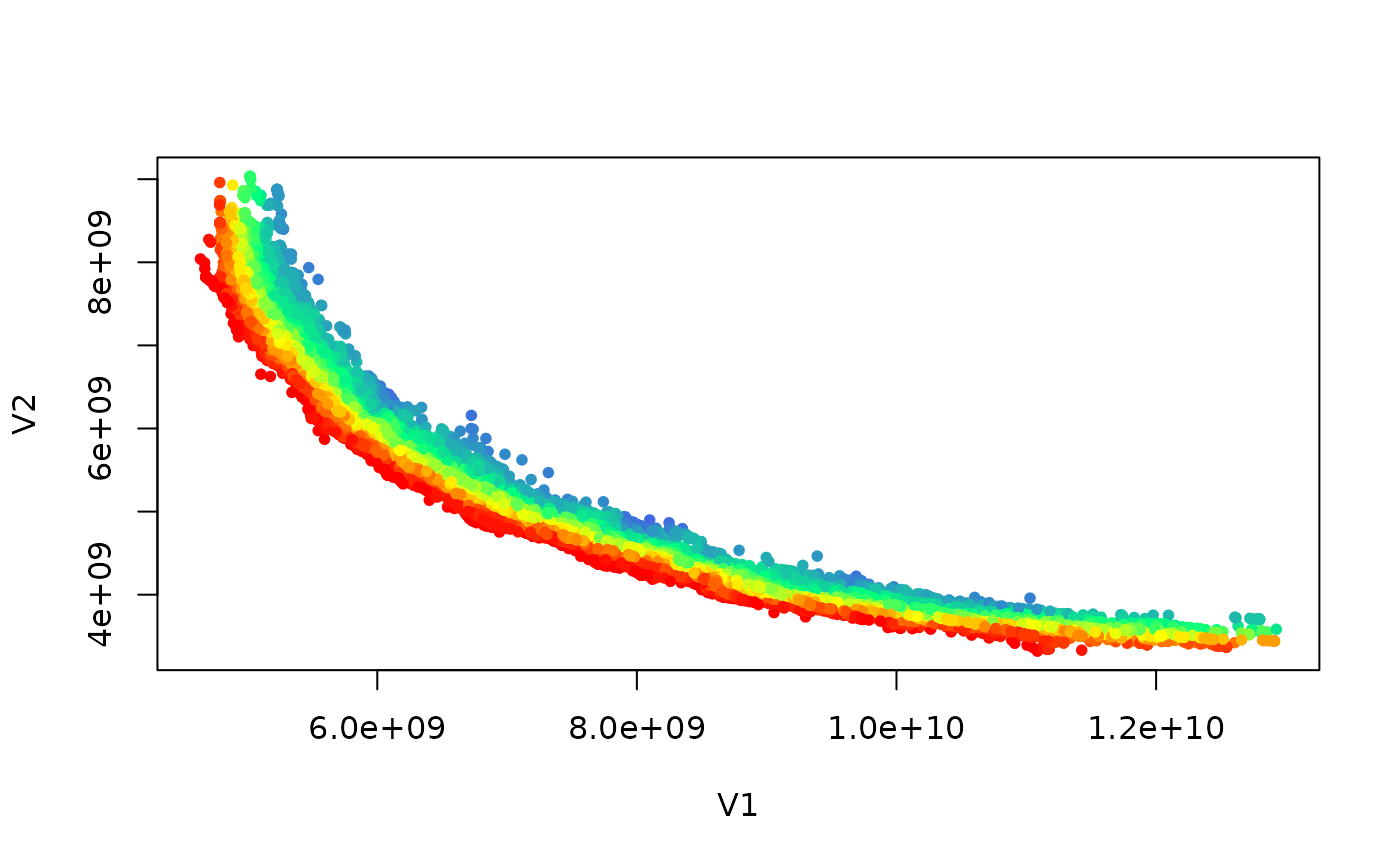Identify, remove and rank dominated points according to Pareto optimality

Identify nondominated points with is_nondominated() and remove dominated ones with filter_dominated().

any_dominated() quickly detects if a set contains any dominated point.

pareto_rank() ranks points according to Pareto-optimality, which is also called nondominated sorting (Deb et al. 2002) .

Usage

is_nondominated(x, maximise = FALSE, keep_weakly = FALSE)

filter_dominated(x, maximise = FALSE, keep_weakly = FALSE)

any_dominated(x, maximise = FALSE, keep_weakly = FALSE)

pareto_rank(x, maximise = FALSE)

Arguments

x: matrix()|data.frame()
Matrix or data frame of numerical values, where each row gives the coordinates of a point.
maximise: logical()
Whether the objectives must be maximised instead of minimised. Either a single logical value that applies to all objectives or a vector of logical values, with one value per objective.
keep_weakly: logical(1)
If FALSE, return FALSE for any duplicates of nondominated points, except the last one.

Value

is_nondominated() returns a logical vector of the same length as the number of rows of data, where TRUE means that the point is not dominated by any other point.

filter_dominated() returns a matrix or data.frame with only mutually nondominated points.

any_dominated() returns TRUE if x contains any (weakly-)dominated points, FALSE otherwise.

pareto_rank() returns an integer vector of the same length as the number of rows of data, where each value gives the rank of each point.

Details

Given \(n\) points of dimension \(m\), the current implementation uses the well-known \(O(n \log n)\) dimension-sweep algorithm (Kung et al. 1975) for \(m \leq 3\) and the naive \(O(m n^2)\) algorithm for \(m \geq 4\). The best-known \(O(n(\log_2 n)^{m-2})\) algorithm for \(m \geq 4\) (Kung et al. 1975) is not implemented yet.

pareto_rank() is meant to be used like rank(), but it assigns ranks according to Pareto dominance, where rank 1 indicates those solutions not dominated by any other solution in the input set. Duplicated points are kept on the same front. The resulting ranking can be used to partition points into a list of matrices, each matrix representing a nondominated front (see examples below)

Let \(m\) be the number of dimensions, i.e., ncol(data)2. With \(m=2\), the code uses the \(O(n \log n)\) algorithm by Jensen (2003) . When \(m=3\), it uses a \(O(k\cdot n \log n)\) algorithm, where \(k\) is the number of fronts in the output. With higher dimensions, it uses the naive \(O(k m n^2)\) algorithm.

References

Kalyanmoy Deb, A Pratap, S Agarwal, T Meyarivan (2002). “A fast and elitist multi-objective genetic algorithm: NSGA-II.” IEEE Transactions on Evolutionary Computation, 6(2), 182–197. doi:10.1109/4235.996017 .

M T Jensen (2003). “Reducing the run-time complexity of multiobjective EAs: The NSGA-II and other algorithms.” IEEE Transactions on Evolutionary Computation, 7(5), 503–515.

H T Kung, F Luccio, F P Preparata (1975). “On Finding the Maxima of a Set of Vectors.” Journal of the ACM, 22(4), 469–476. doi:10.1145/321906.321910 .

Author

Manuel López-Ibáñez

Examples

S = matrix(c(1,1,0,1,1,0,1,0), ncol = 2, byrow = TRUE)
is_nondominated(S)
#> [1] FALSE  TRUE  TRUE FALSE
is_nondominated(S, maximise = TRUE)
#> [1]  TRUE FALSE FALSE FALSE
filter_dominated(S)
#>      [,1] [,2]
#> [1,]    0    1
#> [2,]    1    0
filter_dominated(S, keep_weakly = TRUE)
#>      [,1] [,2]
#> [1,]    0    1
#> [2,]    1    0
#> [3,]    1    0
any_dominated(S)
#> [1] TRUE
any_dominated(S, keep_weakly = TRUE)
#> [1] TRUE
any_dominated(filter_dominated(S))
#> [1] FALSE

three_fronts = matrix(c(1, 2, 3,
                        3, 1, 2,
                        2, 3, 1,
                        10, 20, 30,
                        30, 10, 20,
                        20, 30, 10,
                        100, 200, 300,
                        300, 100, 200,
                        200, 300, 100), ncol=3, byrow=TRUE)
pareto_rank(three_fronts)
#> [1] 1 1 1 2 2 2 3 3 3

split.data.frame(three_fronts, pareto_rank(three_fronts))
#> $`1`
#>      [,1] [,2] [,3]
#> [1,]    1    2    3
#> [2,]    3    1    2
#> [3,]    2    3    1
#> 
#> $`2`
#>      [,1] [,2] [,3]
#> [1,]   10   20   30
#> [2,]   30   10   20
#> [3,]   20   30   10
#> 
#> $`3`
#>      [,1] [,2] [,3]
#> [1,]  100  200  300
#> [2,]  300  100  200
#> [3,]  200  300  100
#> 
path_A1 <- file.path(system.file(package="moocore"),"extdata","ALG_1_dat.xz")
set <- read_datasets(path_A1)[,1:2]
is_nondom <- is_nondominated(set)
cat("There are ", sum(is_nondom), " nondominated points\n")
#> There are  583  nondominated points

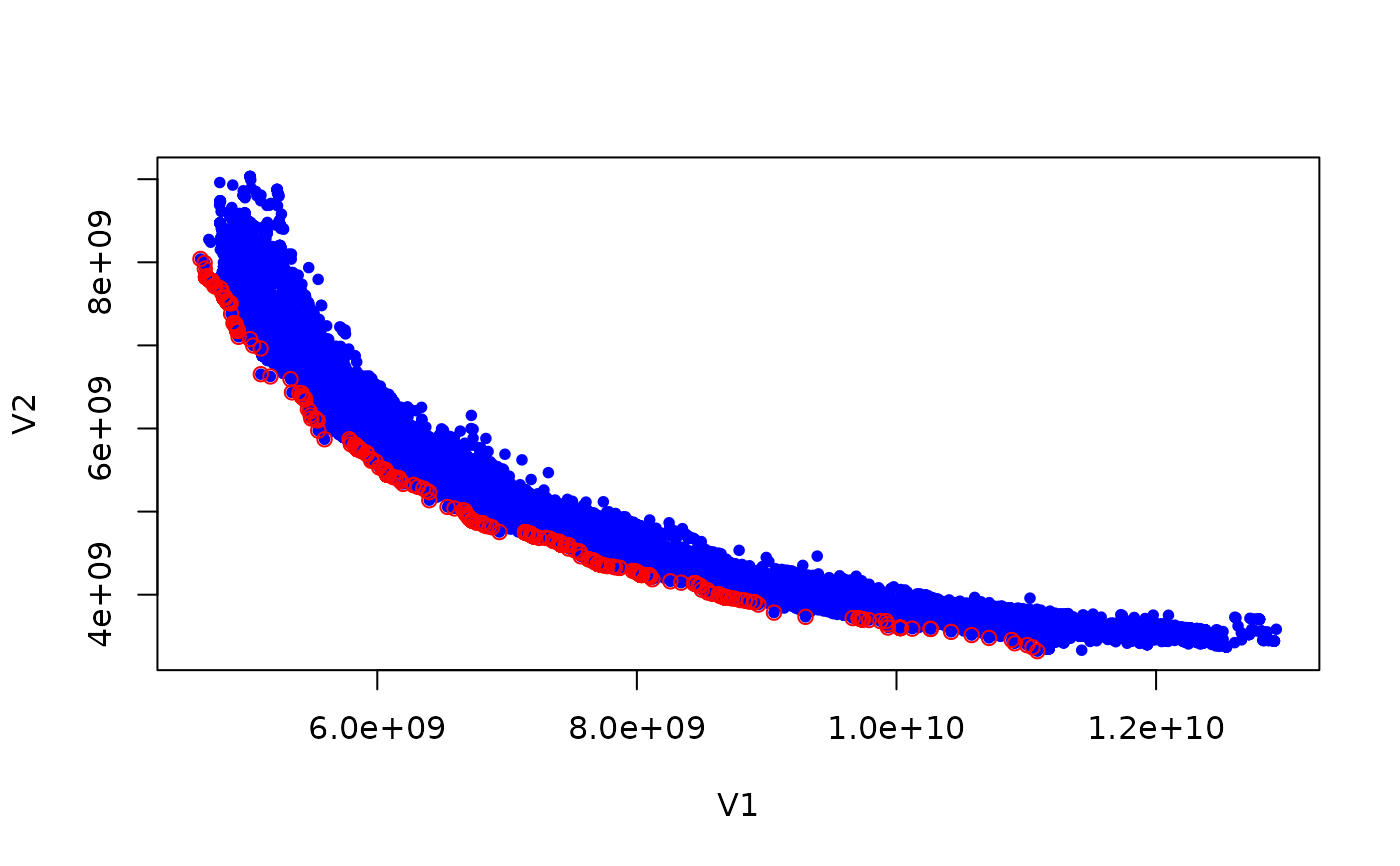
if (requireNamespace("graphics", quietly = TRUE)) {
   plot(set, col = "blue", type = "p", pch = 20)
   ndset <- filter_dominated(set)
   points(ndset[order(ndset[,1]),], col = "red", pch = 21)
}


ranks <- pareto_rank(set)
str(ranks)
#>  int [1:23260] 13 24 20 22 22 5 23 5 16 20 ...
if (requireNamespace("graphics", quietly = TRUE)) {
   colors <- colorRampPalette(c("red","yellow","springgreen","royalblue"))(max(ranks))
   plot(set, col = colors[ranks], type = "p", pch = 20)
}