moocore: Core Algorithms for Multi-Objective Optimization#
Version: 0.2.0.dev0 (What’s new)
Date Dec 29, 2025
Useful links: Install | Source Repository | Issue Tracker
This webpage documents the moocore Python package. There is also a moocore R package.
The goal of the moocore project (multi-objective/moocore) is to collect and document fast implementations of core mathematical functions and algorithms for multi-objective optimization and make them available to different programming languages via similar interfaces. These functions include:
Quality metrics such as (weighted) hypervolume, epsilon, IGD+, etc.
Computation of the Empirical Attainment Function. The empirical attainment function (EAF) describes the probabilistic distribution of the outcomes obtained by a stochastic algorithm in the objective space.
Most critical functionality is implemented in C, with the R and Python packages providing convenient interfaces to the C code.
Keywords: empirical attainment function, summary attainment surfaces, EAF differences, multi-objective optimization, bi-objective optimization, performance measures, performance assessment
The reference guide contains a detailed description of the functions, modules, and objects.
Detailed examples and tutorials.
Benchmarks#
The following plots compare the performance of moocore, pymoo, BoTorch, DESDEO, paretoset, Nevergrad, jMetalPy, seqme, fast-pareto and Optuna. Other Python packages are not included in the comparison because they are based on these packages for the functionality benchmarked, so they are at least as slow as them. For example Xopt and BoFire use BoTorch, pysamoo is an extension of pymoo, DESDEO already uses moocore for hypervolume and other quality metrics, and most of the multi-objective functionality of DEAP is shared by pymoo. We do not compare with the Bayesian optimization toolbox trieste, because it is much slower than BoTorch and too slow to run the benchmarks in a reasonable time.
Not all packages provide the same functionality. For example, pymoo does not provide the epsilon indicator whereas jMetalPy does not provide the IGD+ indicator. BoTorch provides neither of them. paretoset and fast-pareto only identify nondominated points.
The source code for the benchmarks below can be found at multi-objective/moocore .
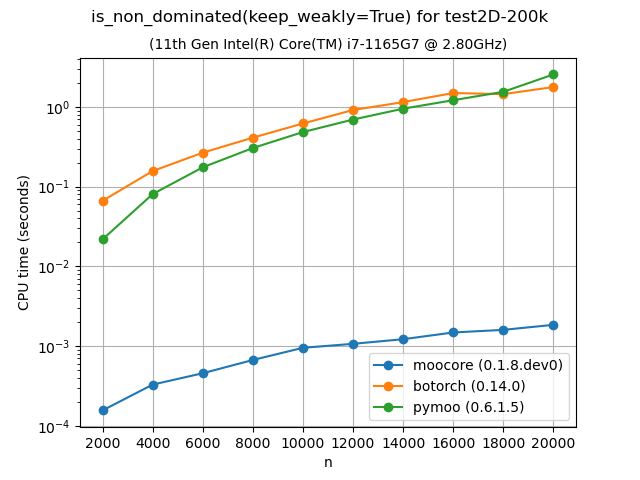
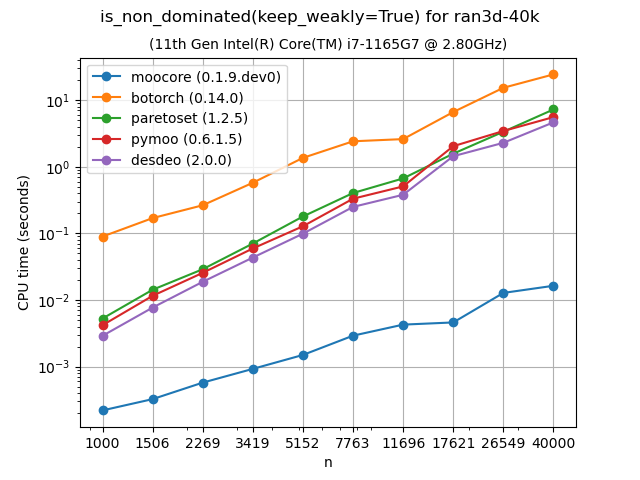
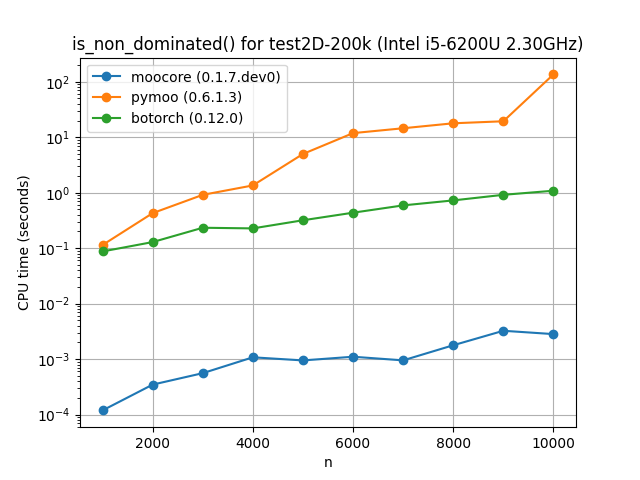
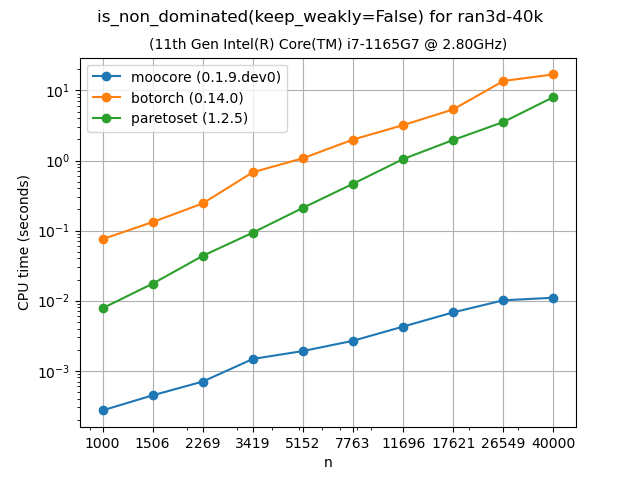
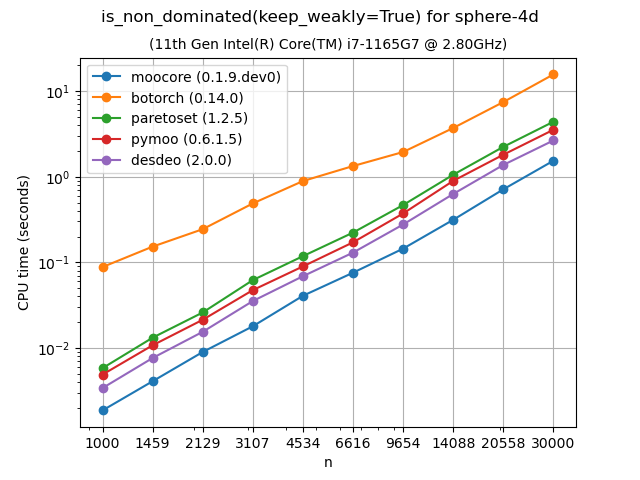
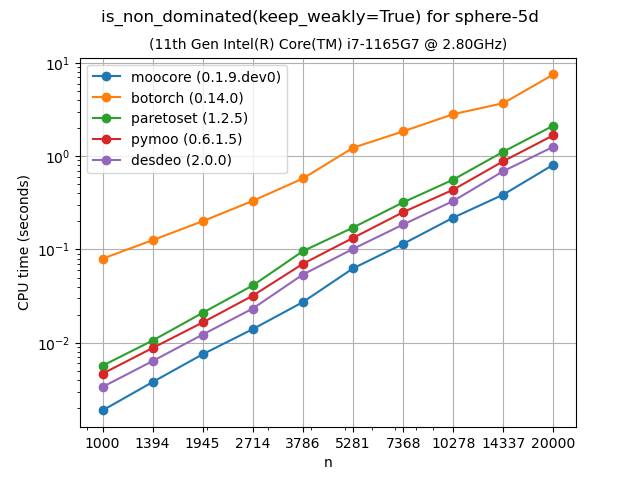
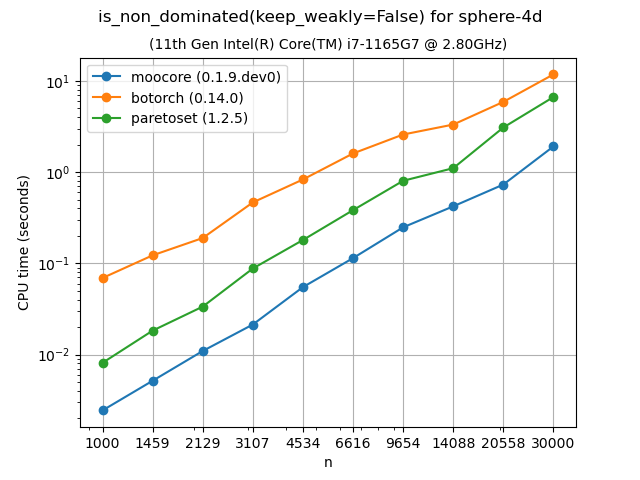
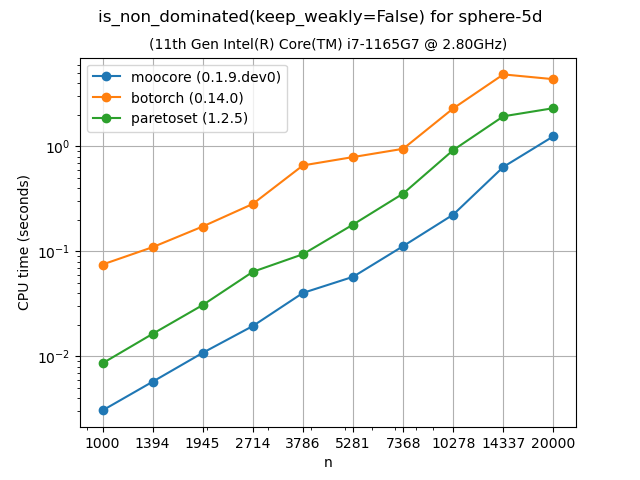
Identifying nondominated points#
The following plots compare the speed of finding nondominated solutions, equivalent to moocore.is_nondominated(), in 2D and 3D. We test both keep_weakly=True and keep_weakly=False (the latter is only supported by botorch and paretoset). The plots show that moocore is 10 times faster than DESDEO and paretoset and 100 times faster than the other packages. fast-pareto claims to implement a \(O(n\log n)\) algorithm for 3D, but the benchmarks below indicate a \(O(n^2)\) complexity, similar to other packages and significantly slower than moocore.
For dimensions larger than 3, moocore.is_nondominated() still uses the
naive \(O(m n^2)\) algorithm. Nevertheless, the plots show that moocore
is still consistently faster than the other packages. fast-pareto claims to be using a \(O(n\log^{m-2} n)\) algorithm, but the benchmarks suggest that it is also using a \(O(m n^2)\) algorithm, although slower than most other packages and almost 10 times slower than moocore.
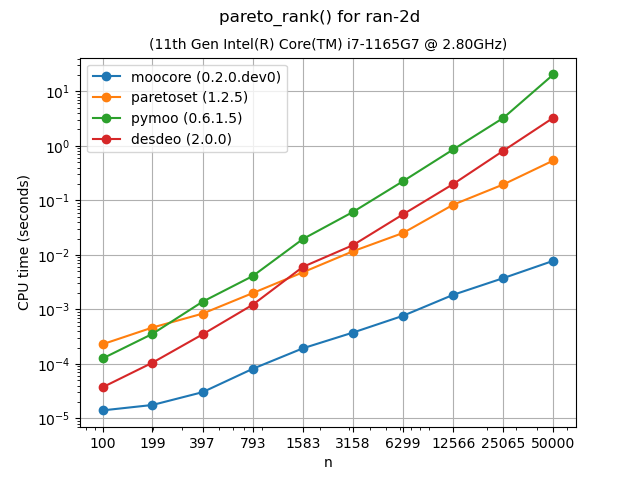
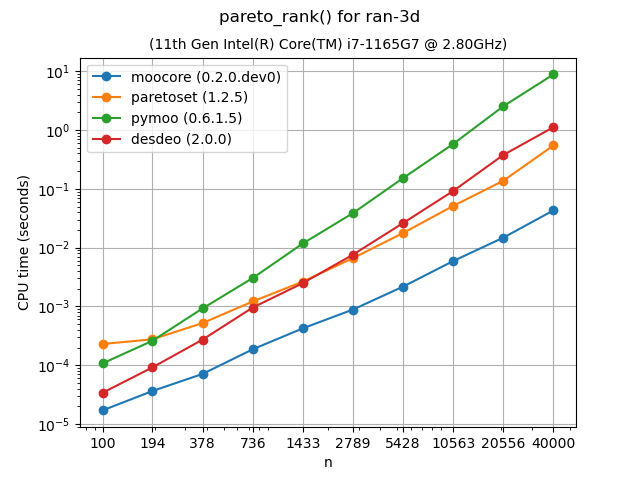
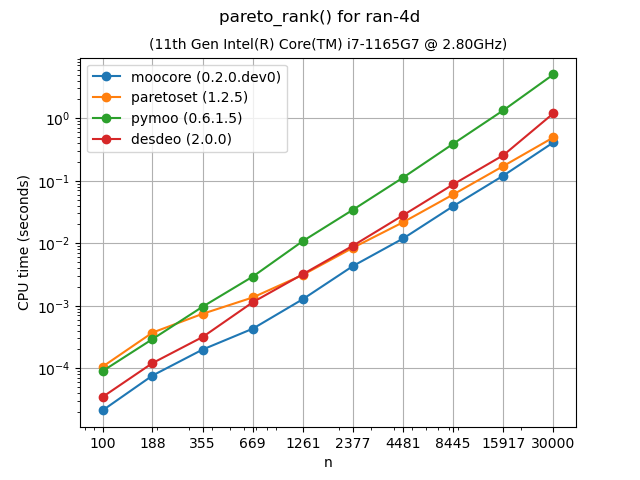
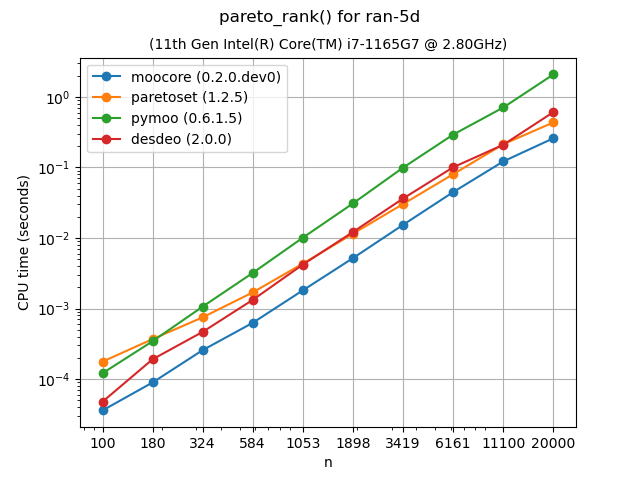
Nondominated Sorting (Pareto ranking)#
Nondominated sorting (or Pareto ranking) assigns a rank to each point according
to Pareto-optimality. It can be used to split a set of points into layers of
nondominated fronts. For more details, see moocore.pareto_rank(). This
function in moocore uses a \(O(n \log n)\) algorithm for 2 dimensions
and a \(O(k\cdot n\log n)\) algorithm for 3 dimensions. As the plots show,
this makes moocore significantly faster than paretoset, pymoo and
DESDEO. With higher dimensions, moocore uses the naive \(O(k m
n^2)\) algorithm, similar to paretoset and DESDEO (if the latter are
compiled with Numba). In these benchmarks points are sampled uniformly at
random within the hyper-cube.
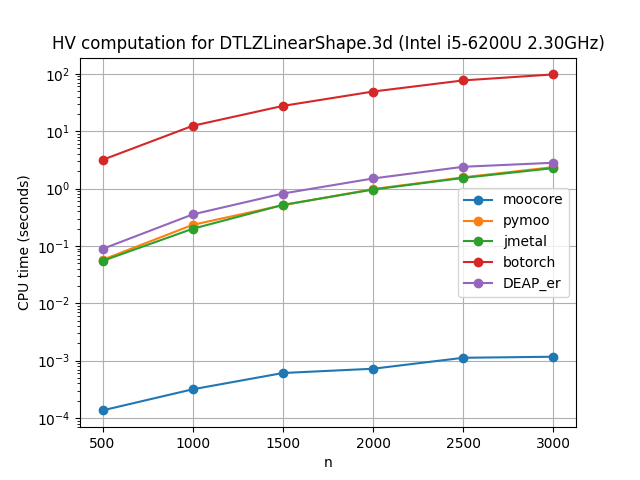
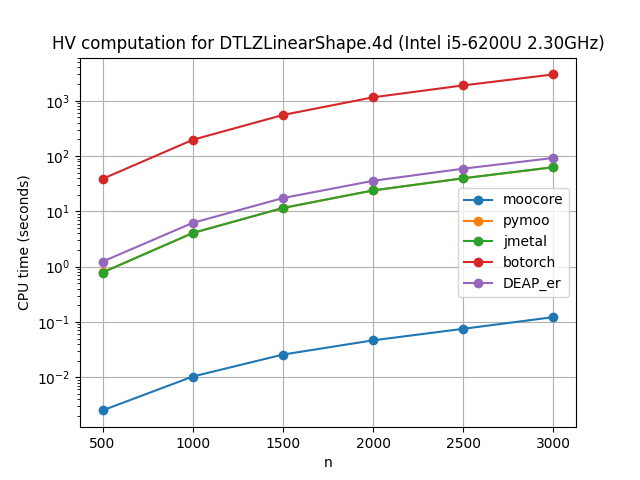
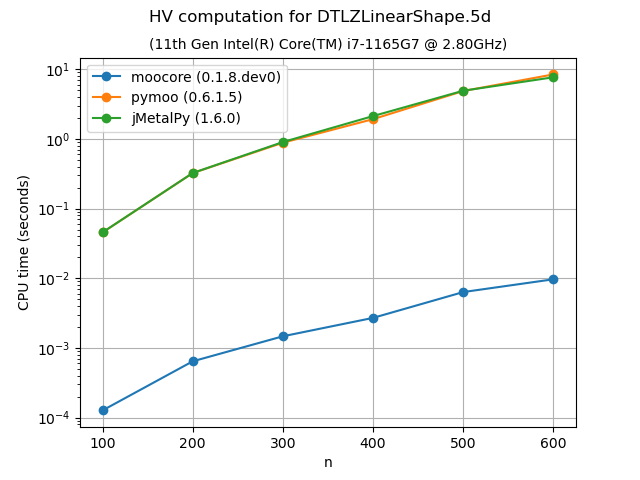
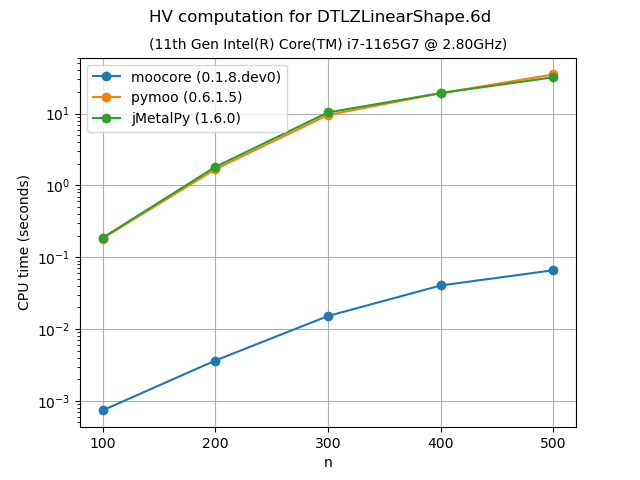
Exact computation of hypervolume#
The following plots compare the speed of computing the hypervolume indicator in 3D, 4D, 5D and 6D. As the plots show, moocore is 100 times faster than the other packages and 1000 times faster than BoTorch and, by extension, Xopt and BoFire.
For 3D, Optuna uses a \(O(n^2)\) algorithm, while moocore uses the best-known \(O(n\log n)\) one, so the gap between the two will get significantly larger with a larger number of points than those tested here. BoTorch and fast-pareto are not included for more than 3 objectives because they are tens of thousands of times slower than moocore. Nevergrad and Optuna are not included for more than 5 objectives for the same reason.
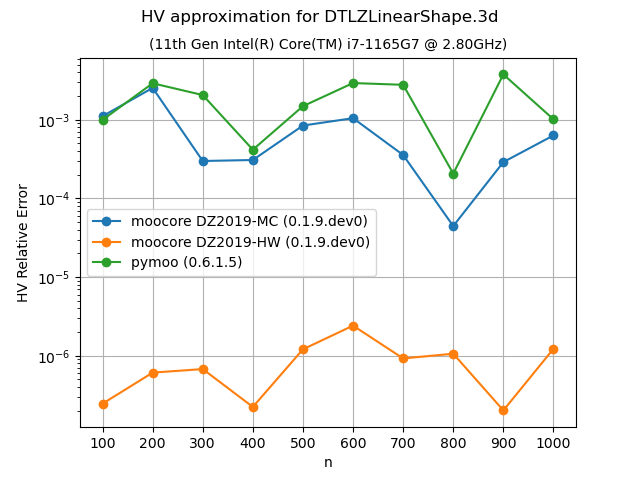
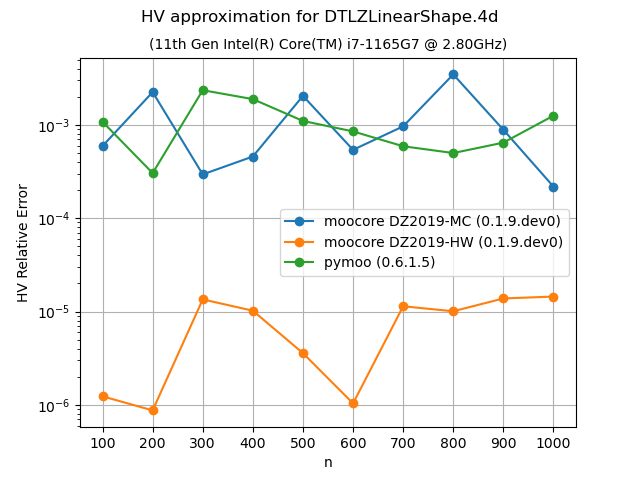
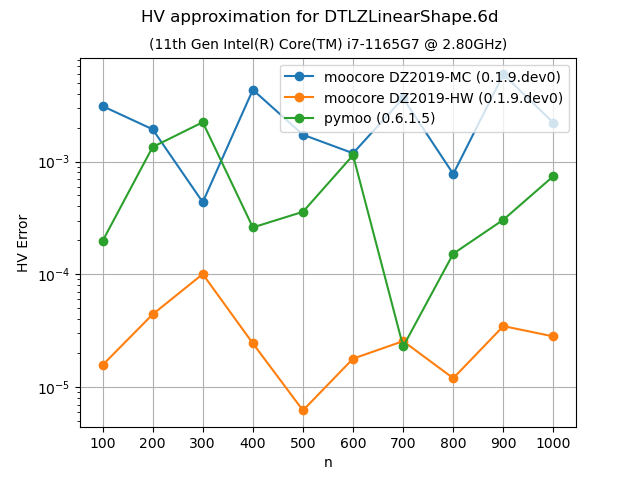
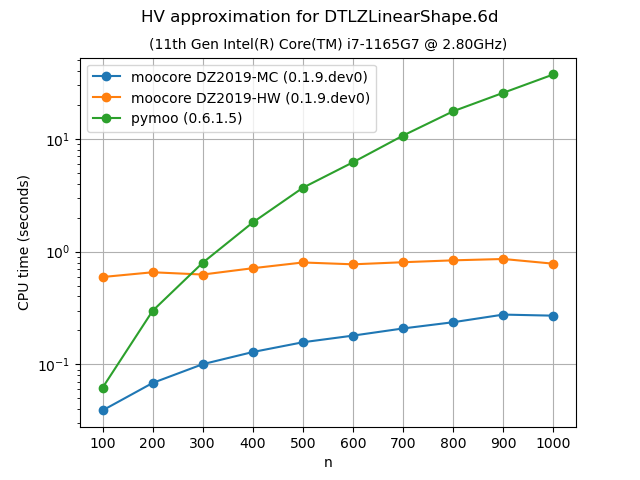
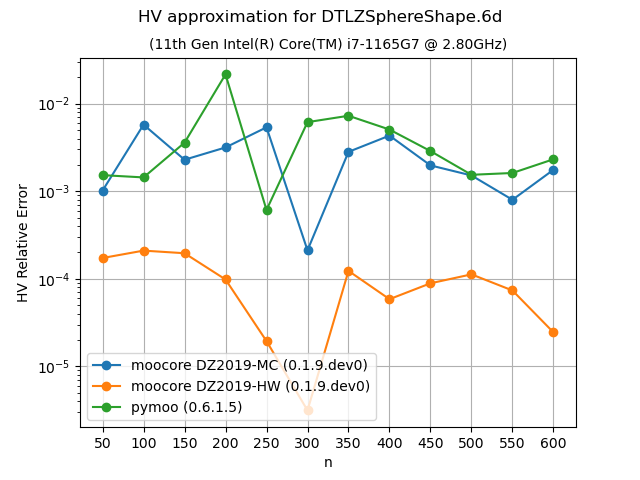
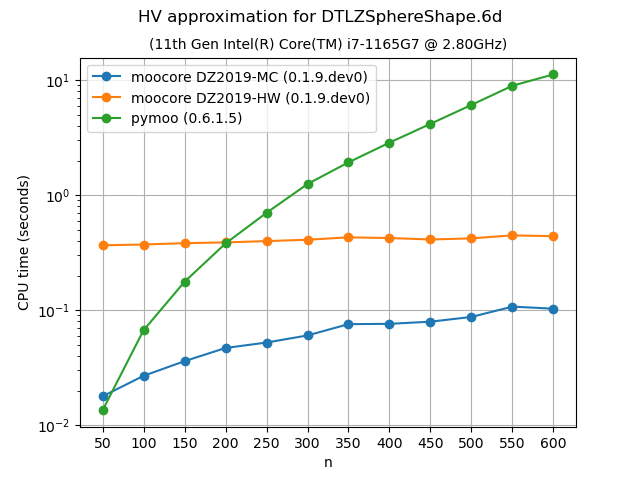
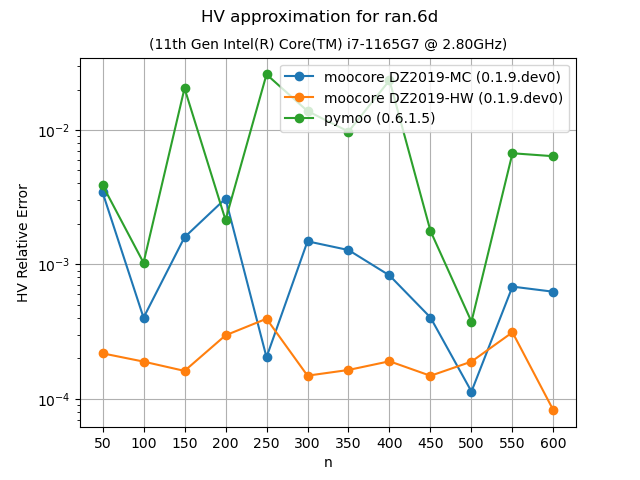
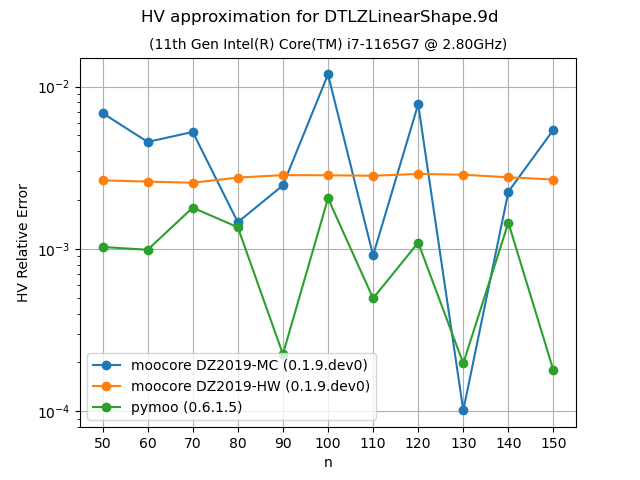
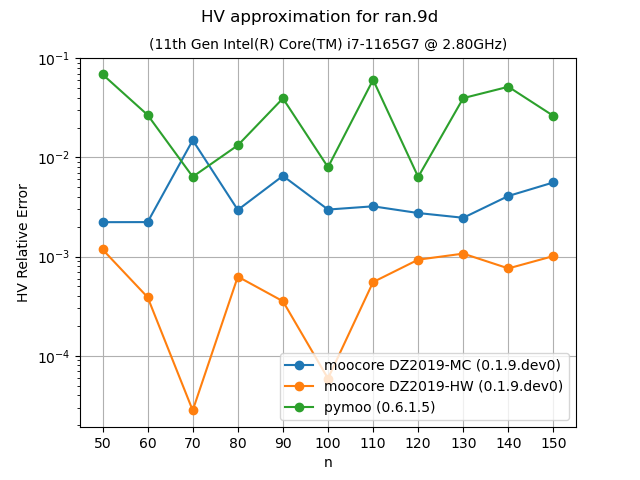
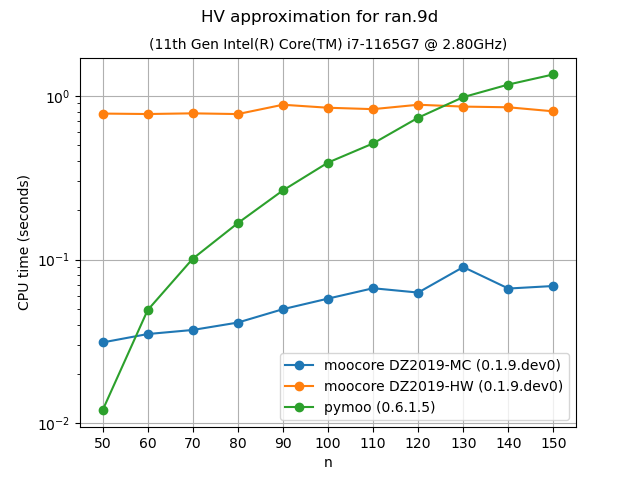
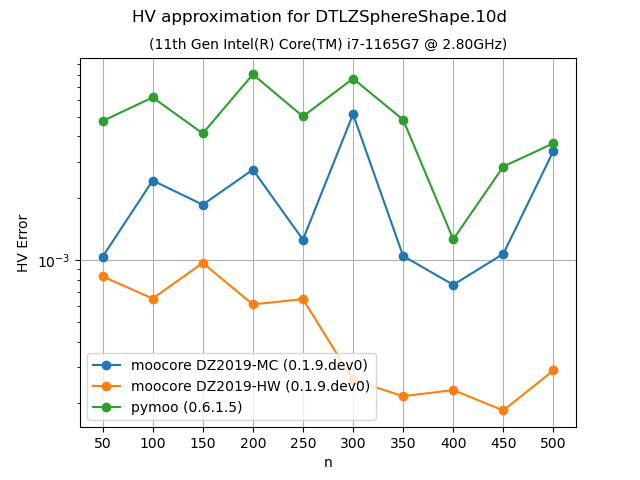
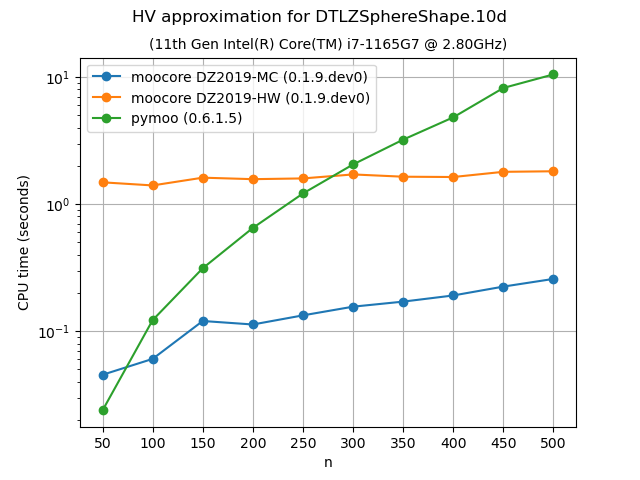
Approximation of the hypervolume#
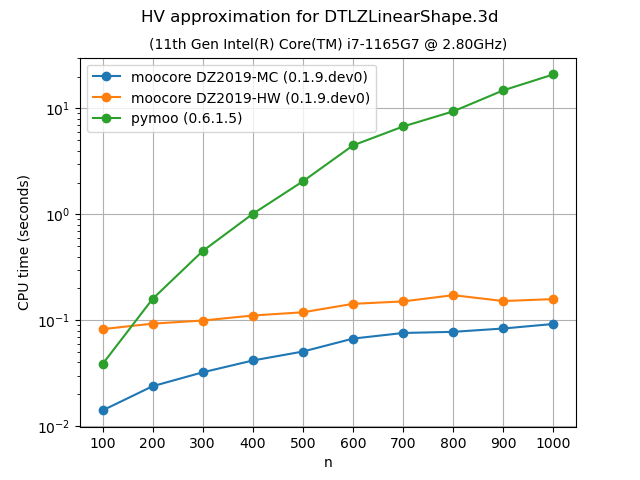
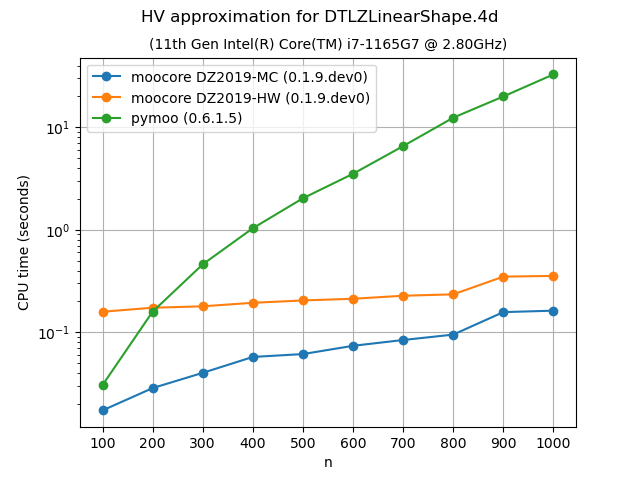
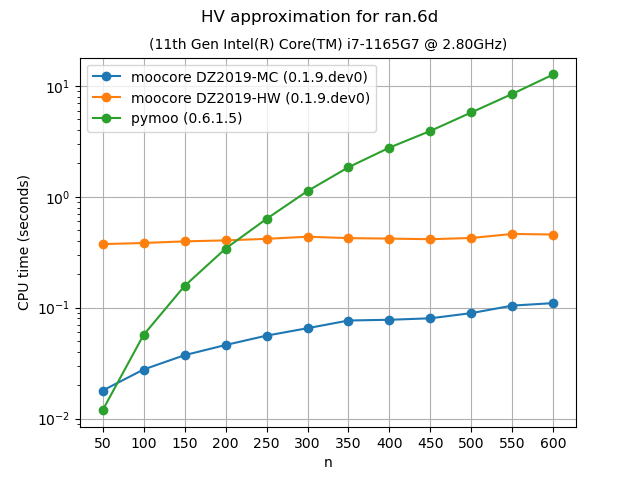
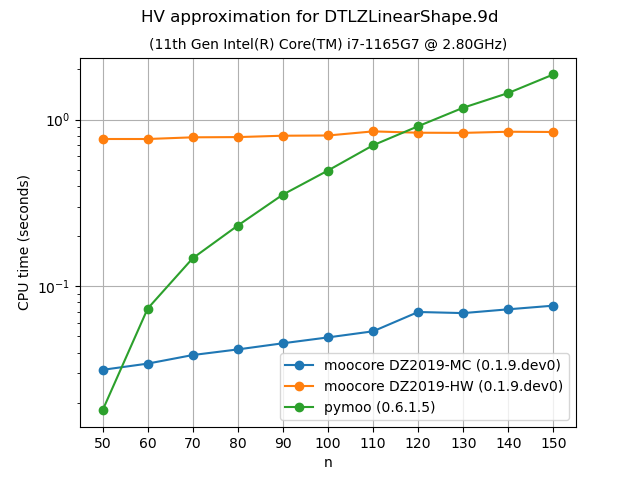
The following plots compare the accuracy and speed of approximating the hypervolume with the various methods provided by moocore.hv_approx(). The plots show that method DZ2019-HW consistently produces the lowest approximation error, but it is also slower than method DZ2019-MC. When the number of points increases, both methods are significantly faster than pymoo.
If you compare the plots of DTLZLinearShape-3d and DTLZLinearShape-4d below to the ones above in the previous section, you can see that the exact computation of the hypervolume in 3D or 4D for thousands of points takes milliseconds, whereas approximating the hypervolume is significantly slower and, thus, not worth doing.
Approximating the hypervolume becomes more useful for dimensions higher than 5, where the exact computation becomes noticeably slower with hundreds of points. For such problems, method DZ2019-HW is significantly slower for few points than pymoo, which is much slower than DZ2019-MC. However, the computation time of DZ2019-HW increases very slowly with the number of points whereas the computation time of pymoo increases very rapidly.
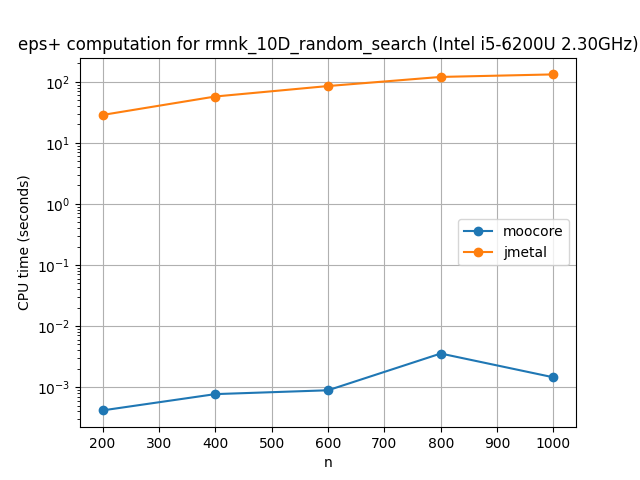
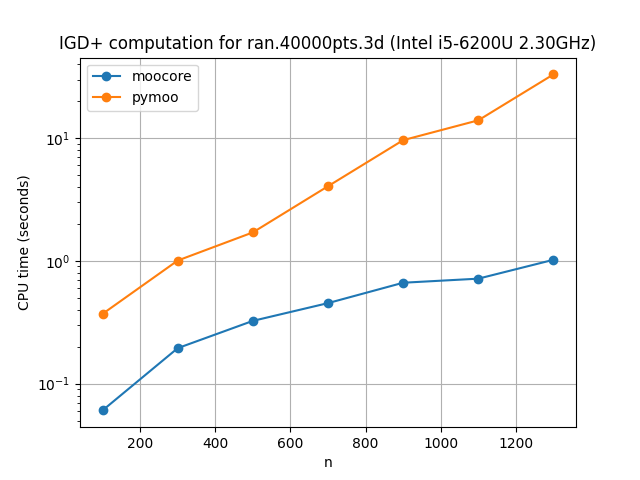
Epsilon and IGD+ indicators#
The following plots compare the speed of computing the epsilon indicator metric and IGD+ indicator. Although the algorithms for computing these metrics are relatively simple and easy to vectorize in Python, the moocore implementation is still 10 to 100 times faster. The implementation of IGD+ in DESDEO is almost a thousand times slower than moocore, so it is not included in the benchmarks below.