generate_ndset#

moocore.generate_ndset(n, d, /, method, *, seed=None, integer=False)[source]#

Generate a random set of n mutually nondominated points of dimension d with the shape defined by method.

When integer=False (the default), the points are generated within the hypercube \((0,1)^d\) and can be scaled to another range using normalise(). Otherwise, points are scaled to a non-negative integer range that keeps the points mutually nondominated.

Parameters:

  • n (int) – Number of rows in the output.

  • d (int) – Number of columns in the output.

  • method (str) – Method used to generate the random nondominated set. See the Notes below for more details.

  • seed (int | Generator | None, default: None) – Either an integer to seed numpy.random.default_rng(), Numpy default random number generator (RNG) or an instance of a Numpy-compatible RNG. None uses the equivalent of a random seed (see numpy.random.default_rng()).

  • integer (default: False) – Return integer values.

Returns:

ndarray – A 2D nondominated array.

Notes

The methods available are:

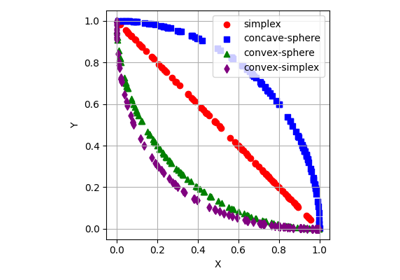
  • "simplex", "linear" or "L": Uniformly samples points on the standard simplex.

  • "concave-sphere", "sphere" or "C": Uniformly samples points on the positive orthant of the hyper-sphere, which is concave for minimisation problems.

  • "convex-sphere" or "X": Equivalent to 1. - generate_ndset("concave-sphere", n, d, seed), which is convex for minimisation problems.

  • "convex-simplex": Equivalent to generate_ndset("concave-sphere", n, d, seed) ** 4, which is convex for minimisation problems. Such a set cannot be obtained by any affine transformation of a subset of the hyper-sphere.

Method "simplex" uniformly samples points on the standard simplex. The standard \((d-1)\)-simplex is defined by \(\{\vec{x}\in \mathbb{R}_+^d : \sum_{i=1}^d x_i = 1\}\). This shape of nondominated set is also called linear in the literature [1]. Points are generated by the method given by Rubinstein and Melamed[2]. That is, each point \(\vec{z} \in (0,1)^d \subset \mathbb{R}^d\) is generated by sampling \(d\) independent and identically distributed values \((x_1,x_2, \dots, x_d)\) from the exponential distribution, then dividing each value by the l1-norm of the vector, \(z_i = x_i / \sum_{i=1}^d x_i\). Values sampled from the exponential distribution are guaranteed to be positive.

Method "concave-sphere" uniformly samples points on the positive orthant of the hyper-sphere, which is concave when all objectives are minimised. Points are generated by the method proposed by Muller[3]. That is, each point \(\vec{z} \in (0,1)^d \subset \mathbb{R}^d\) is generated by sampling \(d\) independent and identically distributed values \(\vec{x}=(x_1,x_2, \dots, x_d)\) from the standard normal distribution, then dividing each value by the l2-norm of the vector, \(z_i = \frac{|x_i|}{\|\vec{x}\|_2}\). The absolute value in the numerator ensures that points are sampled on the positive orthant of the hyper-sphere.

Method "convex-sphere" is quivalent to 1. - generate_ndset("concave-sphere", n, d, seed), which is convex for minimisation problems. It corresponds to translating points from the negative orthant of the hyper-sphere to the positive orthant.

Method "convex-simplex" is equivalent to generate_ndset("concave-sphere", n, d, seed)**4, which is convex for minimisation problems. The corresponding surface is equivalent to a simplex curved towards the origin.

Methods "simplex", "concave-sphere" and "convex-sphere" are different from the similar ones suggested by Lacour et al.[1]. The latter methods sample values from a uniform distribution before projecting the values to a simplex or hyper-sphere, which does not result in a uniform sampling on the projection surface.

References

Examples

>>> moocore.generate_ndset(5, 3, "simplex", seed=42)
array([[0.33742524, 0.32787894, 0.33469582],
       [0.15382676, 0.047522  , 0.79865124],
       [0.30561291, 0.67719985, 0.01718724],
       [0.47441115, 0.03192912, 0.49365973],
       [0.51684378, 0.11549762, 0.3676586 ]])
>>> moocore.generate_ndset(5, 3, "simplex", seed=42, integer=True)
array([[21, 20, 21],
       [ 9,  3, 51],
       [19, 43,  1],
       [30,  2, 31],
       [33,  7, 23]])
>>> rng = np.random.default_rng(42)
>>> moocore.generate_ndset(4, 2, "sphere", seed=rng)
array([[0.28118049, 0.9596549 ],
       [0.62368072, 0.78167919],
       [0.83175713, 0.5551397 ],
       [0.37478326, 0.92711246]])
>>> moocore.generate_ndset(3, 5, "convex-sphere", seed=rng)
array([[0.98843533, 0.41282763, 0.39468745, 0.46462554, 0.95454935],
       [0.37787475, 0.74198125, 0.52575586, 0.79648617, 0.47079199],
       [0.47186748, 0.96998408, 0.88885902, 0.5906188 , 0.26499673]])
>>> moocore.generate_ndset(4, 4, "convex-simplex", seed=rng)
array([[1.50912692e-03, 8.90810874e-02, 4.06920896e-02, 2.12488882e-01],
       [6.92170773e-04, 1.12617206e-03, 1.33695589e-03, 8.16435071e-01],
       [1.26387422e-02, 3.18954020e-02, 2.03159622e-01, 6.66944487e-02],
       [2.27337966e-01, 2.35916000e-05, 6.97235603e-02, 6.46639006e-02]])