Computing Multi-Objective Quality Metrics

Several examples of computing multi-objective unary quality metrics.

import numpy as np
import moocore

Comparing two multi-objective datasets using unary quality metrics

First, read the datasets.

spherical = moocore.get_dataset("spherical-250-10-3d.txt")
uniform = moocore.get_dataset("uniform-250-10-3d.txt")

spherical_objs = spherical[:, :-1]
spherical_sets = spherical[:, -1]
uniform_objs = uniform[:, :-1] / 10
uniform_sets = uniform[:, -1]

Create reference set and reference point.

ref_set = moocore.filter_dominated(np.vstack((spherical_objs, uniform_objs)))
ref_point = 1.1

Calculate metrics.

uniform_igd_plus = moocore.apply_within_sets(
    uniform_objs, uniform_sets, moocore.igd_plus, ref=ref_set
)
spherical_igd_plus = moocore.apply_within_sets(
    spherical_objs, spherical_sets, moocore.igd_plus, ref=ref_set
)

uniform_epsilon = moocore.apply_within_sets(
    uniform_objs, uniform_sets, moocore.epsilon_mult, ref=ref_set
)
spherical_epsilon = moocore.apply_within_sets(
    spherical_objs, spherical_sets, moocore.epsilon_mult, ref=ref_set
)

uniform_hypervolume = moocore.apply_within_sets(
    uniform_objs, uniform_sets, moocore.hypervolume, ref=ref_point
)
spherical_hypervolume = moocore.apply_within_sets(
    spherical_objs, spherical_sets, moocore.hypervolume, ref=ref_point
)

print(f"""
            Uniform       Spherical
            -------       ---------
Mean HV  :  {np.mean(uniform_hypervolume):.5f}       {np.mean(spherical_hypervolume):.5f}
Mean IGD+:  {np.mean(uniform_igd_plus):.5f}       {np.mean(spherical_igd_plus):.5f}
Mean eps*:  {np.mean(uniform_epsilon):.3f}       {np.mean(spherical_epsilon):.3f}

""")

            Uniform       Spherical
            -------       ---------
Mean HV  :  0.78689       0.73290
Mean IGD+:  0.12383       0.15745
Mean eps*:  623.278       225.916

IGD and Average Hausdorff are not Pareto-compliant

Example 4 by Ishibuchi et al.¹ shows a case where IGD gives the wrong answer.

ref = np.array([10, 0, 6, 1, 2, 2, 1, 6, 0, 10]).reshape(-1, 2)
A = np.array([4, 2, 3, 3, 2, 4]).reshape(-1, 2)
B = np.array([8, 2, 4, 4, 2, 8]).reshape(-1, 2)

Assuming minimization of both objectives, A is better than B in terms of Pareto optimality.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()

df = pd.concat(
    [
        pd.DataFrame({"f1": x[:, 0], "f2": x[:, 1], "Set": label})
        for x, label in zip([ref, A, B], ["Ref", "A", "B"])
    ],
    ignore_index=True,
)
ax = sns.scatterplot(data=df, x="f1", y="f2", style="Set", hue="Set", s=200)
plt.show()

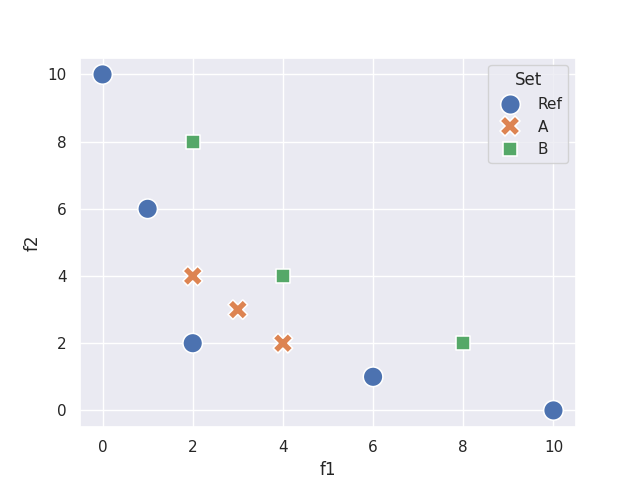
However, both moocore.igd() and moocore.avg_hausdorff_dist() incorrectly measure B as better than A, whereas moocore.igd_plus() and moocore.hypervolume() correctly measure A as better than B (remember that hypervolume must be maximized) and moocore.epsilon_additive() measures both as equally good (epsilon is weakly Pareto compliant).

pd.DataFrame(
    dict(
        A=[
            moocore.igd(A, ref),
            moocore.avg_hausdorff_dist(A, ref),
            moocore.igd_plus(A, ref),
            moocore.epsilon_additive(A, ref),
            moocore.hypervolume(A, ref=10),
        ],
        B=[
            moocore.igd(B, ref),
            moocore.avg_hausdorff_dist(B, ref),
            moocore.igd_plus(B, ref),
            moocore.epsilon_additive(B, ref),
            moocore.hypervolume(B, ref=10),
        ],
    ),
    index=["IGD", "Hausdorff", "IGD+", "eps+", "HV"],
)

	A	B
IGD	3.707092	2.591483
Hausdorff	3.707092	2.591483
IGD+	1.482843	2.260113
eps+	2.000000	2.000000
HV	61.000000	44.000000