Computing Multi-Objective Quality Metrics • moocore

Several examples of computing multi-objective unary quality metrics.

library(moocore)
library(dplyr, warn.conflicts=FALSE)
get_dataset <- function(filename)
  read_datasets(system.file(file.path("extdata", filename),
    package = "moocore", mustWork = TRUE))
apply_within_sets <- function(x, sets, FUN, ...) {
  FUN <- match.fun(FUN)
  sapply(X = split.data.frame(x, sets), FUN = FUN, ...)
}

Comparing two multi-objective datasets using unary quality metrics

First, read the datasets:

spherical <- get_dataset("spherical-250-10-3d.txt")
uniform <- get_dataset("uniform-250-10-3d.txt")

spherical_objs <- spherical[, -ncol(spherical)]
spherical_sets <- spherical[, ncol(spherical)]
uniform_objs <- uniform[, -ncol(uniform)] / 10
uniform_sets <- uniform[, ncol(uniform)]

Create reference set and reference point:

ref_set <- filter_dominated(rbind(spherical_objs, uniform_objs))
ref_point <- 1.1

Calculate metrics:

uniform_igd_plus <- apply_within_sets(uniform_objs, uniform_sets,
  igd_plus, ref = ref_set)
spherical_igd_plus <- apply_within_sets(spherical_objs, spherical_sets,
  igd_plus, ref = ref_set)

uniform_epsilon <- apply_within_sets(uniform_objs, uniform_sets,
  epsilon_mult, ref = ref_set)
spherical_epsilon <- apply_within_sets(spherical_objs, spherical_sets,
  epsilon_mult, ref = ref_set)

uniform_hypervolume <- apply_within_sets(uniform_objs, uniform_sets,
  hypervolume, ref = ref_point)
spherical_hypervolume <- apply_within_sets(spherical_objs, spherical_sets,
  hypervolume, ref = ref_point)

knitr::kable(data.frame(
  Uniform = c(mean(uniform_hypervolume), mean(uniform_igd_plus),
    mean(uniform_epsilon)),
  Spherical = c(mean(spherical_hypervolume), mean(spherical_igd_plus),
    mean(spherical_epsilon)),
  row.names = c("Mean HV","Mean IGD+","Mean eps*")), format = "html") %>%
  kableExtra::kable_styling(position = "center",
    bootstrap_options = c("striped", "condensed", "responsive"))

	Uniform	Spherical
Mean HV	0.7868862	0.7328974
Mean IGD+	0.1238303	0.1574521
Mean eps*	623.2775539	225.9158914

IGD and Average Hausdorff are not Pareto-compliant

Example 4 by Ishibuchi et al. (2015) shows a case where IGD gives the wrong answer:

ref <- matrix(c(10, 0, 6, 1, 2, 2, 1, 6, 0, 10), ncol = 2, byrow=TRUE)
A <- matrix(c(4, 2, 3, 3, 2, 4), ncol = 2, byrow=TRUE)
B <- matrix(c(8, 2, 4, 4, 2, 8), ncol = 2, byrow=TRUE)

par(mar = c(4, 4, 1, 1)) # Reduce empty margins
plot(ref, xlab=expression(f[1]), ylab=expression(f[2]),
  panel.first=grid(nx=NULL), pch=23, bg="gray", cex=1.5)
points(A, pch=1, cex=1.5)
points(B, pch=19, cex=1.5)
legend("topright", legend=c("Reference", "A", "B"), pch=c(23,1,19),
  pt.bg="gray", bg="white", bty = "n", pt.cex=1.5, cex=1.2)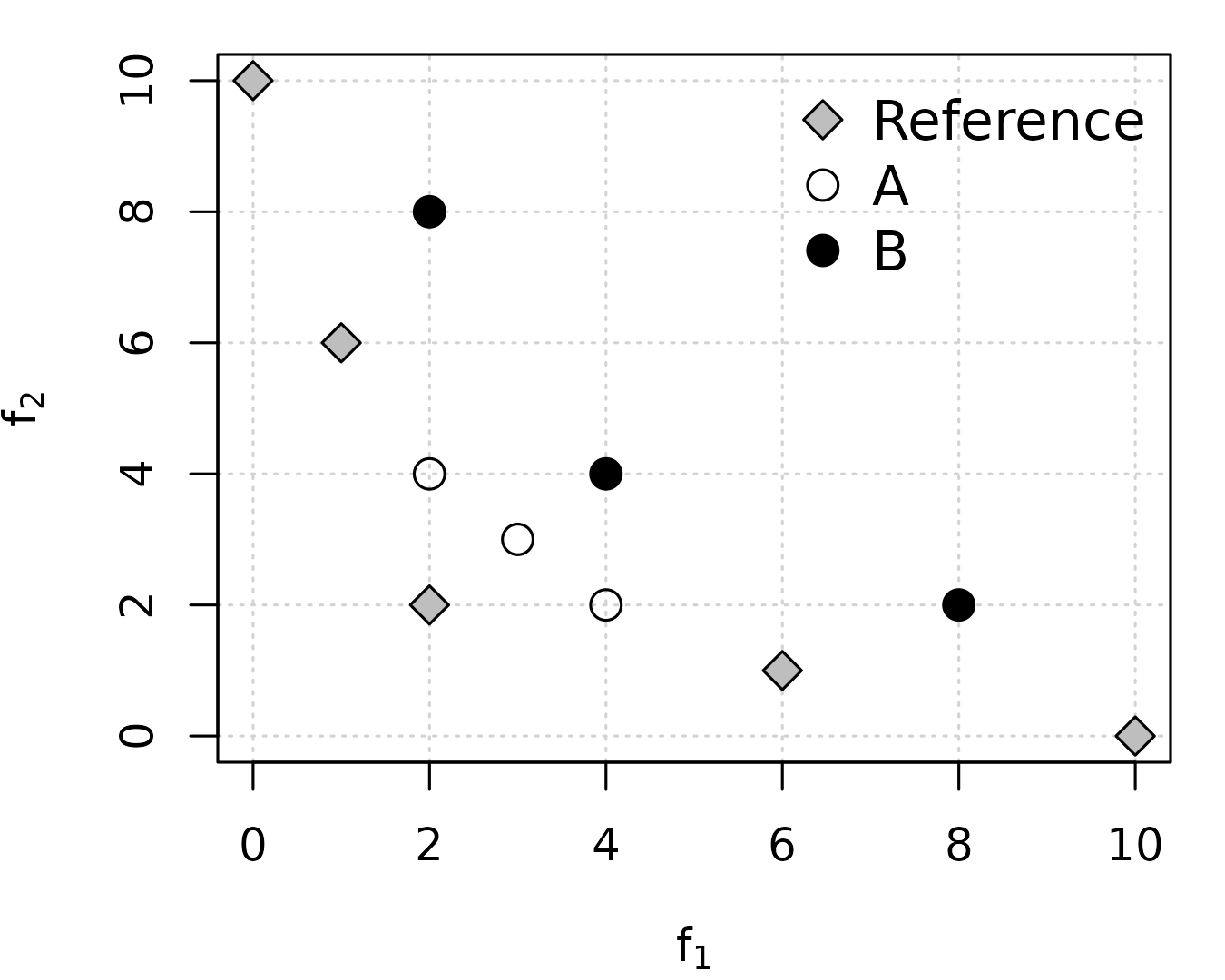

Assuming minimization of both objectives, $A$ is better than $B$ in terms of Pareto optimality. However, both igd() and avg_hausdorff_dist() incorrectly measure $B$ as better than $A$ , whereas r2_exact(), igd_plus() and hypervolume() correctly measure $A$ as better than $B$ (remember that hypervolume must be maximized) and epsilon_additive() measures both as equally good (epsilon is weakly Pareto compliant).

knitr::kable(
  data.frame(
    A = c(
        igd(A, ref),
        avg_hausdorff_dist(A, ref),
        igd_plus(A, ref),
        epsilon_additive(A, ref),
        hypervolume(A, ref=10),
        r2_exact(A, ref=0)),
    B = c(
        igd(B, ref),
        avg_hausdorff_dist(B, ref),
        igd_plus(B, ref),
        epsilon_additive(B, ref),
        hypervolume(B, ref=10),
        r2_exact(B, ref=0)),
    row.names=c("IGD", "Hausdorff", "IGD+", "eps+", "HV", "Exact R2")), format = "html") %>%
  kableExtra::kable_styling(position = "center",
    bootstrap_options = c("striped", "condensed", "responsive"))

	A	B
IGD	3.707092	2.591483
Hausdorff	3.707092	2.591483
IGD+	1.482843	2.260113
eps+	2.000000	2.000000
HV	61.000000	44.000000
Exact R2	1.630952	2.066667

References

Ishibuchi, Hisao, Hiroyuki Masuda, Yuki Tanigaki, and Yusuke Nojima. 2015. “Modified Distance Calculation in Generational Distance and Inverted Generational Distance.” In Evolutionary Multi-Criterion Optimization, EMO 2015 Part I, edited by António Gaspar-Cunha, Carlos Henggeler Antunes, and Carlos A. Coello Coello, 9018:110–25. Lecture Notes in Computer Science. Heidelberg, Germany: Springer.